Page d'Accueil
- Galerie d'Animations 3D
- Tutoriel POV-Ray
Animation 3D
Table des matières
0. Bases.
1. Exemple du base.
2. Example 2.
3. D'Images à gif animé.
4. D'Images à Vidéo.
5. Connaissance de base.
6. Commandes d'animation.
I. Animations cycliques.
1. Objets tournants.
1.2. Planètes en orbite.
1.3. Une horloge
2. Caméra tournante.
2.1. Caméra deplacée linéaire
3. Le problème
de la roue.
3.1. Roues roulantes.
4. Engrenages.
4.1. Chaîne à rouleaux.
4.2. Chaîne de bicyclette.
5. Balancement.
5.1. Pendule de Newton
5.2. Rock le rocking chair !
6. Oscillation.
7. Bielle d'accouplement
7.1. Bielle et manivelle.
8. Psychédélique + Op-Art.
9. Compteurs
+ Compte à rebours
10. La pliage d'un cube.
II. Mouvements non-linéaires
> 1.0 Accélérer et ralentir 1.
1.1 Accélérer et ralentir 2.
2. Chuter et bondir.
3. Accélération selon
formules physiques.
4. Mouvements
avec fonctions spline.
III. Chemins pour
des animations avec
des courbes spline
1. Courbes spline.
2. Spline fermé.
3. Animation Paths.
|
 |
Accélérer et ralentir (1).
Mouvements non-linéaires en animations pour accélérations et décélérations réalistes avec des fonctions de base en POV-Ray. |
|
La simulation realiste de
accélération et décélération
4 macro très utiles :
//---------------------------
#macro Cos_01( X )
(0.5-0.5*cos( pi*X))
#end
//---------------------------
#macro Cos_010( X )
(0.5-0.5*cos(2*pi*X))
#end
//---------------------------
#macro Cos_10( X )
(1-(0.5-0.5*cos( pi*X)))
#end
//---------------------------
#macro Cos_101( X )
(1-(0.5-0.5*cos( 2*pi*X)))
#end
//---------------------------
|
|
macro 'Cos_01( TIME )'
Départ doux, arrivée douce.
macro 'Cos_010( TIME )'
Départ doux, retour doux,
et arrivée douce.
|
macro 'Cos_10( TIME )'
Départ doux, arrivée douce.
macro 'Cos_101( TIME )'
Départ doux, retour doux,
et arrivée douce.
|
|
|
Ici quelques examples comment utiliser :
|
#macro Cos_010( X ) //------------
(0.5-0.5*cos(2*pi*X))
#end //---------------------------
// hard
#object{ Tower // left
translate<2,0,1+3*clock>}
// smooth
#object{ Tower // right
translate<3,0,1+3*Cos_01(clock)>}
//--------------------------------
|
|
Mouvoir abrupt (à gauche) et doucement (à droite)
Le fichier della scène pour POV-Ray:
"Move_hard_n_smooth_1.ini"
and
"Move_hard_n_smooth_1.pov"
|
#macro Cos_010( X ) //-----
(0.5-0.5*cos(2*pi*X))
#end //--------------------
#declare Fold_Angle =
-90*Cos_010(clock);
//-------------------------
|
Pour un fichier della scène completète et plus des détails:
Développement de Cube.
|
macro 'Cos_101( TIME )'
Départ doux, retour doux,
et arrivée douce.
|
Développement de Cube sans
accélération
|
|
Note:
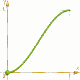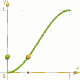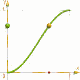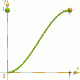
Utiliser des fonctions exponentielles comme
1/(1+exp(-X*A+A/2)), avec A >=10,
est une approximation mathematicalment plus correcte, mais le problem ici :
le valeurs de début et de fin ne sont pas exactement y=0 et y=1 !
C'est (0.5-0.5*cos(2*pi*X)) est l'approximation meilleure !
Aussi f(X)= 3*X*X - 2*X*X*X ha f(0)= 0, f(1)= 1 et f'(0)=f'(1)=0.
Pour movements avec début et fin à v=0 et a=0, une fonction avec la dérivation second = 0 au debut à la fin,
comme f(X)= 6*X5 -15*X4 +10*X3 = X*X*X*(10+X*(6*X-15))
est une approximation plus parfait !
|
1/(1+exp(-X*10+10/2))
|
0.5-0.5*cos(2*pi*X)
|
X*X*X*(10+X*(6*X-15))
|
|