Home
- Animationen Galerie
- POV-Ray Tutorial
3D Animation
Inhaltsübersicht
0. Grundlagen
1. Beispiel
2. Beispiel 2
3. Bilder zu animierte Gif
4. Von Bildern zum Video
5. Grundbegriffe
6. Animationsbefehle
I. Zyklische Animationen
1. Objekt-Rotation
1.2. Planeten im Orbit
1.3. Animierte Uhr
2. Kamera-Rotation
2.1. Kamera Geradeausflug
3. Western-Kutschen
-Problem
3.1. Rollende Räder
4. Zahnradgetriebe
4.1. Rollende Kette
4.2. Fahrradkette
5. Pendelschwingung
5.1. Newtonpendel
5.2: Schaukelstuhl
6. Federpendel
7. Koppelstange
7.1. Pleuelstange
8. Psychedelic + Op-Art
9. Zähler + Countdowns
10. Faltung eines Würfels
II. Nichtlineare Bewegungen
> 1.0 Beschleunigung
+ Bremsen 1
> 1.1 Beschleunigung
+ Bremsen 2
2. Fallen + Hüpfen
3. Beschleunigung nach
physikalischen Formeln
4. Geschwindigkeitssteuerung
mit Spline-Funktionen
III. Animationspfade
mit Spline-Kurven
1. Spline-Kurven
2. Geschlossene Splines
3. Animationspfade
|
 |
Beschleunigung und Abbremsen (1)
Nichtlineare Bewegungen in Animationen zur realistischen Beschleunigung und Verzögerung mittels elementarer Funktionen in POV-Ray. |
|
Realistische Simulation von
Beschleunigung und Verzögerung
4 nützlliche Makros:
//---------------------------
#macro Cos_01( X )
(0.5-0.5*cos( pi*X))
#end
//---------------------------
#macro Cos_010( X )
(0.5-0.5*cos(2*pi*X))
#end
//---------------------------
#macro Cos_10( X )
(1-(0.5-0.5*cos( pi*X)))
#end
//---------------------------
#macro Cos_101( X )
(1-(0.5-0.5*cos( 2*pi*X)))
#end
//---------------------------
|
|
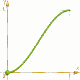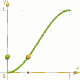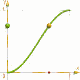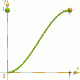
macro 'Cos_01( TIME )'
Start sanft, Ende sanft.
macro 'Cos_010( TIME )'
Start sanft, Umkehr sanft,
und Ende sanft.
|
macro 'Cos_10( TIME )'
Start sanft, Ende sanft.
macro 'Cos_101( TIME )'
Start sanft, Umkehr sanft,
und Ende sanft.
|
|
|
Einige Anwendungsbeispiele:
|
#macro Cos_010( X ) //------------
(0.5-0.5*cos(2*pi*X))
#end //---------------------------
// hard
#object{ Tower // left
translate<2,0,1+3*clock>}
// smooth
#object{ Tower // right
translate<3,0,1+3*Cos_01(clock)>}
//--------------------------------
|
|
Bewegung abrupt (links) und sanft (rechts)
Szenenbeschreibung für POV-Ray:
"Move_hard_n_smooth_1.ini"
und
"Move_hard_n_smooth_1.pov"
|
#macro Cos_010( X ) //-----
(0.5-0.5*cos(2*pi*X))
#end //--------------------
#declare Fold_Angle =
-90*Cos_010(clock);
//-------------------------
|
Für eine komplete Szenendatei und mehr Details siehe:
Faltung eines Würfels.
|
macro 'Cos_101( TIME )'
Start sanft, Umkehr sanft,
und Ende sanft.
|
Faltung ohne
Beschleunigung
|
|
Anmerkung:
Die Verwendung von Exponentialfunktionen wie
1/(1+exp(-X*A+A/2)), mit A >=10,
wäre eine mathematisch genauere Näherung, aber das Problem hier:
Der Start- und der Endpunkt ist nicht genau bei y=0 bzw. y=1!
Daher (0.5-0.5*cos(2*pi*X)) ist eine bessere Näherung!
Auch f(X)= 3*X*X - 2*X*X*X hat f(0)= 0, f(1)= 1 und f'(0)=f'(1)=0.
Bei Bewegungen mit Start und Ende bei v=0 und a=0, ist eine Funktion mit der 2.Ableitung = 0 am Start und am Ende,
wie etwa
f(X)= 6*X5 -15*X4 +10*X3 = X*X*X*(10+X*(6*X-15)),
eine perfektere Approximation!
|
1/(1+exp(-X*10+10/2))
|
0.5-0.5*cos(2*pi*X)
|
X*X*X*(10+X*(6*X-15))
|
|