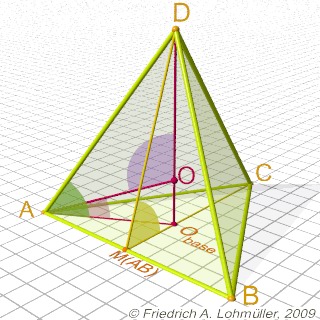
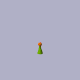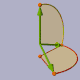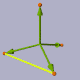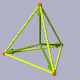Dimensions
Length of tetrahedron edge: a. |
The height
of an regular tetrahedron:
h = sqrt (2/3) * a ;
The radius of circumsphere:
R = sqrt( 3/8 ) * a ;
The height of the incenter O or
the radius of the insphere:
r = 1/3 * R or
r = 1/sqrt(24) * a ;
The radius of midsphere (tangent to edges):
rm = 1/sqrt(8) * a ;
The angle between two faces: ~ 70,53 (yellow)
Angle(C,MAB,D) = degrees(atan(2*sqrt(2)));
The angle between an edge and a face: ~ 54,74 (green)
Angle(0,A,D) = degrees( atan(sqrt(2)));
The angle vertex-center-vertex: ~ 109.471 (violet)
Angle(A,0,D) = degrees( acos( -1/3 ));
|
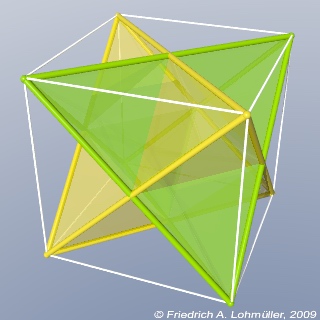
Two regular tetrahedron in a cube
|
A regular tetrahedron
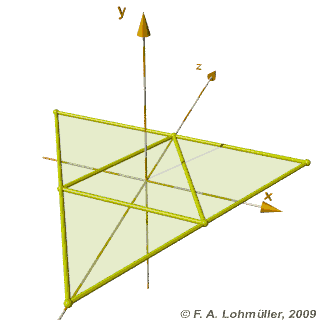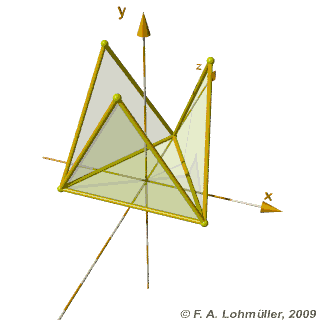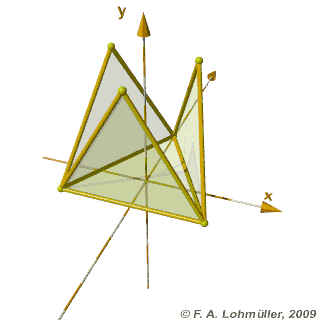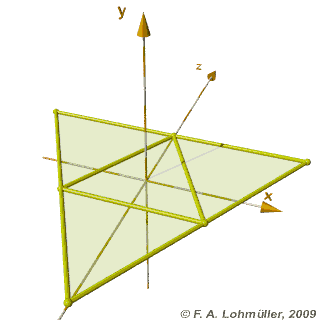
Folding of a regular tetrahedron
A tetrahedron of vectors
How to make it with POV-Ray
Animation in POV-Ray
|