Home
- POV-Ray Tutorial
- POV-Ray Examples
Index of Content
- Geometry
- Pawn
- Wireframe Cube
- Octagon
- Egg Shape
- Star
- Optical Lens
- Chessboard
- Regular Tetrahedron
- Penrose Triangle
- Yin & Yang
- Fishblob
- Threefold
- Trefoil
- Architecture
- Engineering
|
|
Tetrahedron by Vectors
The construction of a tetrahedron by caculating the vectors of the vertices.
Objects: "sphere", "cylinder", "cone".
Methods: "#declare","union", "#macro", "vrotate".
Click here for an example!
- See also my POV-Ray Animation Tetrahedron by Vectors.
|
Elementary Geometrical Facts on Tetrahedron
which are used here:
For more Details see Elementary Geometry on Regular Tetrahedron.
For a regular tetrahedron we can calculate from the side "Side_a"
the radius of the circumsphere:
R_circum = sqrt( 3/8 ) * Side_a;
And the angle between a vertex, the center and an other vertex:
Vertex_Center_Vertex_Angle = degrees(acos(-1/3)); (~ 109.471).
We start by declaring the length of a side of regular tetrahedron "Side_a":
#declare Side_a = 1;
#declare R_circum = sqrt( 3/8 ) * Side_a;
#declare Vertex_Center_Vertex_Angle = degrees( acos( -1/3 )); |
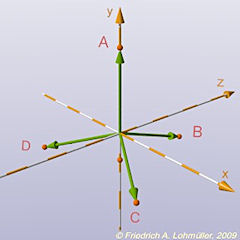
The vectors V1,V2,V3,V4 form <0,0,0> to the corners A,B,C,D:
// caculation of the vectors --------------------------------
#declare V1 = <0,R_circum,0>;
#declare V2 = vrotate( V1,< Vertex_Center_Vertex_Angle,0,0>);
#declare V3 = vrotate( V2,< 0, 120, 0>);
#declare V4 = vrotate( V2,< 0,-120, 0>);
//----------------------------------------------------------- |
For drawing vector symbols we use the following macro:
//---------------------------- macro Vector(Start,End,Radius)
#macro Vector(P_s,P_e, Rv)
union{
cylinder{ P_s, P_e - (vnormalize(P_e - P_s)*9.5*Rv), Rv }
cone { P_e - (vnormalize(P_e - P_s)*10*Rv), 3*Rv, P_e,0}
}// end of union
#end //----------------------------------------- end of macro |
Alternatively: #include "analytical_g.inc"
For drawing vectors to the corners:
#declare Vector_Texture =
texture{ pigment{ color rgb<0.2,0.5,0.0>}
finish { phong 1} }
#declare Rl = 0.01; // line radius
// vectors --------------------------------------------------
object{ Vector( o,V1, Rl) texture{ Vector_Texture }}
object{ Vector( o,V2, Rl) texture{ Vector_Texture }}
object{ Vector( o,V3, Rl) texture{ Vector_Texture }}
object{ Vector( o,V4, Rl) texture{ Vector_Texture }}
//----------------------------------------------------------- |
If we declare the according textures in an analog way we can draw now
the corners, edges and faces:
#declare Corners_Texture =
texture{ pigment{ color rgb<0.75,0.1,0.0>}
finish { phong 1} }
#declare Edge_Texture =
texture{ pigment{ color rgb<1,0.5,0.0>}
finish { phong 1} }
#declare Surface_Texture =
texture{ pigment{ color rgbt<0.3,0.7,0.0, 0.75>}
finish { phong 1} }
#declare Rp = 0.025; // 'point' radius
// corners ------------------------------------------
sphere{ V1, Rp texture{ Corners_Texture } }
sphere{ V2, Rp texture{ Corners_Texture } }
sphere{ V3, Rp texture{ Corners_Texture } }
sphere{ V4, Rp texture{ Corners_Texture } }
// edges --------------------------------------------
cylinder{ V1, V2, Rl texture{ Edge_Texture } }
cylinder{ V2, V3, Rl texture{ Edge_Texture } }
cylinder{ V3, V1, Rl texture{ Edge_Texture } }
cylinder{ V1, V4, Rl texture{ Edge_Texture } }
cylinder{ V2, V4, Rl texture{ Edge_Texture } }
cylinder{ V3, V4, Rl texture{ Edge_Texture } }
// surfaces------------------------------------------
triangle{ V1, V2, V3 texture{ Surface_Texture } }
triangle{ V1, V2, V4 texture{ Surface_Texture } }
triangle{ V2, V3, V4 texture{ Surface_Texture } }
triangle{ V3, V1, V4 texture{ Surface_Texture } }
//--------------------------------------------------- |
|
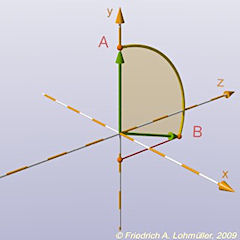
Step 1: rotate VA around x axis by 109.47°.
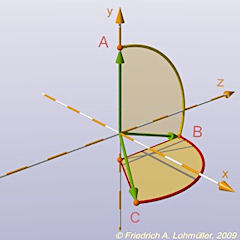
Step 2: rotate VB around y axis by +120°.
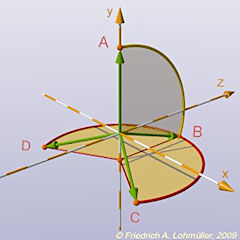
Step 3: rotate VB around y axis by -120°.
The vectors of the corners of the tetrahedron.
Scene description for POV-Ray:
"Regular_Tetrahedron_Vectors_1.pov" or
"Regular_Tetrahedron_Vectors_1.txt"
|
|