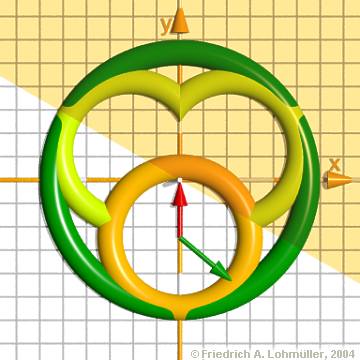
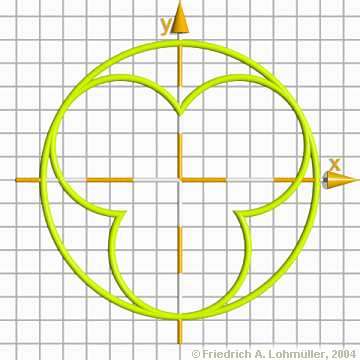
Descriptions and Examples for the POV-Ray Raytracer
by Friedrich A. Lohmüller
POV-Ray Examples -
How To Make Objects for POV-Ray
Français
Deutsch