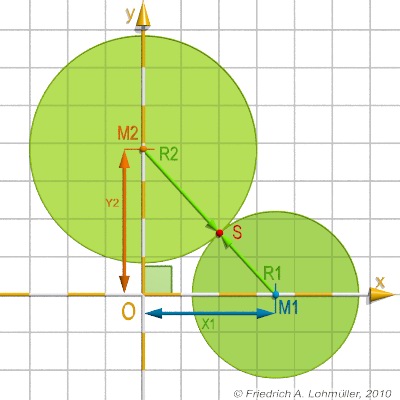
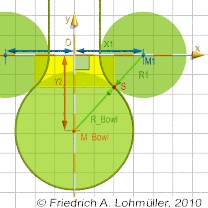
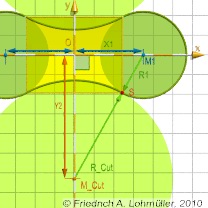
Circle 1: center
M1 = <0.35,0,0>, radius r1= 0.22.
Circle 2: center on y-axis, tangents Circle 1 from outside in the point S. |
Problem 1:
Circle 2 has the radius r2 = 0.30 .
Where on the y-axis (height y2) is the center of the second circle 2 ? (M2 = <0,?,0>)
Problem 2:
Circle 2 has the center M2 = <0,0.40,0>.
How big must be the radius of a second circle 2, if it intersects (touches) the first circle 1 at the nearest point?
Problem 3:
What are the coordinates of the point S ?
Problem 4:
What are the angles at M1 and M2 inside the triangle(0,M1,M2)?
|
The triangle(O,M1,M2) is rectangular!
Therefore we use the Pythagorean Theorem:
// Problem 1: //--------------------------
We know two sides of the triangle(O,M1,M2):
d(0,M1) = x1 and d(M1,M2) = r1+r2.
y2 = sqrt( (r1+r2)2 - x12)
M2 = <0,y2,0>.
// Problem 2: //--------------------------
Because of
r1+r2 = d(M1,M2) = sqrt(x12 + y22),
we get
d(M1,M2) = sqrt( x12 - y22 )
and r2 = d(M1,M2) - r1.
// Problem 3: //--------------------------
There is a simple proportionality:
xS1/xM1 = r2/ (r1+r2) and
yS/yM2 = r1/ (r1+r2),
so: xS = xM1 · r2/ (r1+r2)
yS = yM2 · r1/ (r1+r2).
// Problem 4: //--------------------------
By the inverse trigonometric function i.e. of tan(x):
Angle(M1) = atan ( y2/ x1),
Angle(M2) = 90 - Angle(M1).
|
|
Tangent circles rendered with POV-Ray
Note: To avoid any collision with built-in identifiers and reserved words in POV-Ray,
it's strongly recommanded to use only words beginning with capital letters for all identifiers of variables declared by the user,
i.e. use "R1" instead of "r1"
and use "Y2" instead of "yM2".
#local R1= 0.22;
#local R2= 0.30;
#local M1 = <0.35,0,0>
#local Y2 = sqrt( pow(R1+R2, 2) - pow(M1.x, 2));
#local M2 = <0,Y2,0>; |
Problem 1 in POV-Ray
#local R1= 0.22;
#local M1 = <0.35,0,0>
#local M2 = <0.40,0,0>
#local R2 = sqrt( pow(M1.x,2)-pow(M2.y,2)) - R1;
|
Problem 2 in POV-Ray
#local XS = M1.x * R2/(R1+R2);
#local YS = M2.y * R1/(R1+R2);
#local S = <XS,YS,0>
#local Angle_M1 = degrees( atan( M2.y / M1.x) );
#local Angle_M2 = 90 - Angle_M1; |
Problem 3 + 4 in POV-Ray
|