Home
- POV-Ray Tutorial
- Geometrical Basics
for Raytracing
Right-angled Triangle
Pythagorean Theorem
Trigonometry Basics
Law of cosines
Equilateral Triangle
Regular Polygon
Polyhedron
Tetrahedron
Octahedron
Cube & Cuboid
Dodecahedron
Icosahedron
Cuboctahedron
Truncated Octahedron
Rhombicuboctahedron
Truncated Icosahedron
Circles
Tangent circles
Internal Tangents
External Tangents
- Geometric 3D Animations
|
Trigonometry Basics
sin, cos, tan - Some useful geometrical facts on sine, cosine and tangens |
Note: The trigonometric functions sin(X), cos(X) and tan(X) in POV-Ray
need their arguments X in radians !!! The symbole π = pi in POV-Ray.
|
The units for angles: degrees and radians
The angle in degrees: symbol "°"
The angle by arc length: symbol "rad", often in parts of "pi".
(360° = 2*pi; 180° = pi) |
Conversion of a radiant value RadVal in the according degree value DegVal:
#declare DegVal = degrees(RadVal); or
#declare DegVal = RadVal*(180/pi);
Conversion of a degree value DegVal in the according radiant value RadVal:
#declare RadVal = radians(DegVal); or
#declare RadVal = DegVal*(pi/180);
If we use a value for an angle A in degrees:
#declare SineVal = sin(radians( A ));
The aquivalent is true for the invers functions asin, acos and atan in POV-Ray:
If we want a value for an angle A in degrees:
#declare Angle_in_deg = degrees( asin( 0.50 ));
Otherwise we will get the value in radians:
#declare Angle_in_rad = asin( 0.50 ) ;.
|
|
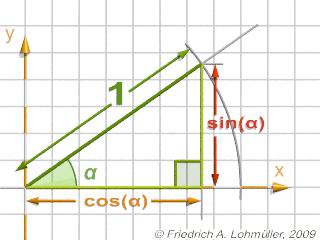
Sine and cosine in a regular triangle
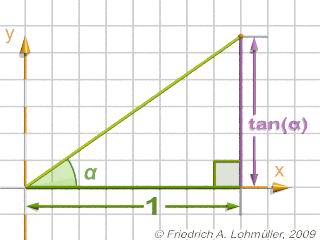
Tangens in a regular triangle
|
|