Beschreibungen und Beispiele zum Raytracer POV-Ray von Friedrich A. Lohmüller

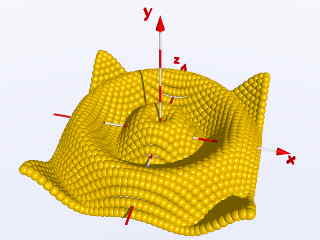
Bisher wurde der Sinus nur in x-Richtung angewandt. Ein besonders reizvoller Effekt ergibt sich jedoch, wenn man die Sinus-Modulation der y-Lage der einzelnen Kugeln von ihrem Abstand von der y-Achse abhängig macht. Hierzu sei daran erinnert, daß der Abstand eines Punktes in kartesischen Koordinaten mittels Pythagoras zu berechnen ist (d.h. Abstand R = Wurzel aus (X Quadrat plus Z Quadrat)! ).

#declare Ball =
 sphere{<0,0,0>,0.25
        texture{pigment{color rgb<1,0.8,0>}
                finish {ambient 0.45 diffuse 0.55 phong 1}
               }// end of texture
       }// end of sphere

#declare Z = -5;    // Start-Wert Z
#declare EndZ = 5;  //   End-Wert Z
#declare Step = 0.5;// Schrittweite

#while ( Z < EndZ + Step)//-------------- Schleifen-Anfang Z

   #declare X = -5;   // Start-Wert X
   #declare EndX = 5; //   End-Wert X
   #while ( X < EndX + Step)//------------ Schleifen-Anfang X

      #declare R = sqrt(X*X+Z*Z)
             //Berechnung des Abstands von der y-Achse
      object{ Ball translate <X,sin(2*R),Z> }
            //abhängig von R moduliert

   #declare X = X + Step; //next X-Wert
   #end // --------------------------------- Schleifen-Ende X

#declare Z = Z + Step; //next Z-Wert
#end // ------------------------------------ Schleifen-Ende Z

Mit
#declare R = sqrt( X * X + Z * Z);
#if (R < 5)
object{Ball translate< X, cos(2*R), Z>}
#end
begrenzt man den Abstand von der y-Achse auf R < 5 und verwendet cos(A) anstelle des Sinus:

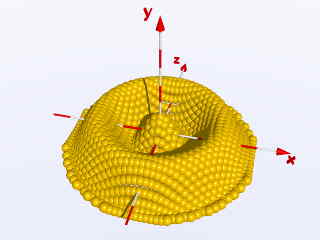
Verkleinert man den Kugelradius und erhöht ihre Dichte so erhöht sich die Kugelzahl schnell beträchtlich - bei folgender Szene sind rund 20 000 Kugeln im Spiel und werden etwa 14 MB RAM benötigt. Zusätzlich wurde der y-Wert der Kugeln umgekehrt proportional zum Abstand R von der Mittelachse moduliert.

#declare Ball =
sphere{<0,0,0>,0.1
       texture{pigment{color rgb<1,0.8,0>}
               finish {ambient 0.45 diffuse 0.55 phong 1}}}
#declare E = 8;
#declare Z = -E;    // Start-Wert Z
#declare EndZ = E;  //   End-Wert Z
#declare Step = 0.1;// Schrittweite
#while ( Z < EndZ + Step)//-------------- Schleifen-Anfang Z

  #declare X = -E;    // Start-Wert X
  #declare EndX = E;  //   End-Wert X
  #while ( X < EndX + Step)//------------ Schleifen-Anfang X
    #declare R = sqrt( X * X + Z * Z);
    #if (R < E)
     object{Ball translate< X, 5/(R+1)*cos(2*R), Z>}
    #end
  #declare X = X + Step; // next X-Wert
  #end // --------------------------------- Schleifen-Ende X

#declare Z = Z + Step; // next Z-Wert
#end // ----------------------------------- Schleifen-Ende Z