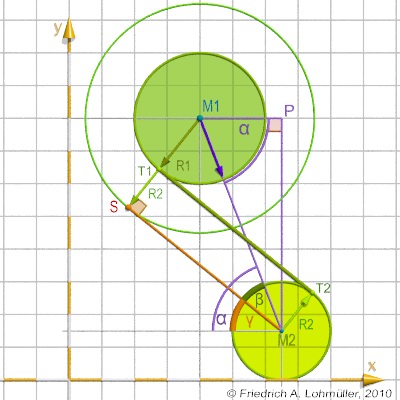
We want an internal tangent to two circles
from T1 to T2, as shown in the opposite image.
Circle 1: M1 = <x1,y1,0>, r1.
Circle 2: M2 = <x2,y2,0>, r2. |
An internal tangent is parallel to a tangent from the center of the smaller circle (here: M2)
to a other circle around the center of the bigger circle (M1) but with the radius r1+r2.
--------------------
For the calulation of the point S we have to calculate the sides of the triangle (M2,M1,S).
d(M1,S) = r1+r2 .
According the Pythagorean Theorem we can calculate:
d(M1,M2) = sqrt((x2-x1)2+(y2-y2)2) .
So the third side (again with the Pythagorean Theorem):
d(M2,S) = sqrt( d(M1,S)2+d(M1,M1)2)
The angle between the direction of (M1,M2) and the x-direction we can find
with trigonometric functions.
If x1 < x2 we have
α = abs(degrees( atan ((y2-y1)/(x2-x1))).
else:
α = 180° - abs(degrees( atan ((y2-y1)/(x2-x1))),
Then we can calulate β and γ as follows:
β = abs( degrees( asin( d(M1, S ) / d(M1,M2) ) )) .
γ = α - β .
The position of T1:
xT1 = x1 - r1·cos( Angle(M1S) ).
yT1 = y1 - r1· sin( Angle(M1S) ).
The position of T2:
xT2 = x2 + r1·cos( Angle(M1S) ).
yT2 = y2 + r1· sin( Angle(M1S) ).
|
|
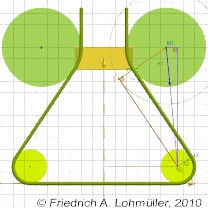
Internal tangent of two circles rendered with POV-Ray
Note: To avoid any collision with built-in identifiers and reserved words in POV-Ray,
it's strongly recommanded to use only words beginning with capital letters for all identifiers of variables declared by the user,
i.e. use "R1" instead of "r1"
and use "Y2" instead of "yM2".
#local X1= 0.40; #local Y1= 0.80; #local R1= 0.20;
#local X2= 0.64; #local Y2= 0.15; #local R2= 0.15;
#local M1 = <X1,Y1,0>; #local M2 = <X2,Y2,0>
//------------------------------------------------
#local M_Dist = sqrt(pow(X2-X1,2)+pow(Y2-Y1,2));
#if ( X1 < X2) #local Alpha =
abs( degrees( atan((Y2-Y1)/(X2-X1))));
#else #local Alpha =
180-abs(degrees(atan((Y2-Y1)/(X2-X1))));
#end
#local Beta = abs(degrees(asin((R1+R2)/M_Dist)));
#local Gamma = Alpha - Beta;
#local T1 = M1-<(R1)*cos( radians(Gamma)),
(R1)*sin( radians(Gamma)),0>;
#local T2 = M2+<(R2)*cos( radians(Gamma)),
(R2)*sin( radians(Gamma)),0>; |
The calulation of the tangent from T1 to T2 in POV-Ray
|