Home
- POV-Ray Tutorial
- Geometrical Basics
for Raytracing
Right-angled Triangle
Pythagorean Theorem
Trigonometry Basics
Law of cosines
Equilateral Triangle
Regular Polygon
Polyhedron
Tetrahedron
Octahedron
Cube & Cuboid
Dodecahedron
Icosahedron
Cuboctahedron
Truncated Octahedron
Rhombicuboctahedron
Truncated Icosahedron
Circles
Tangent circles
Internal Tangents
External Tangents
- Geometric 3D Animations
|
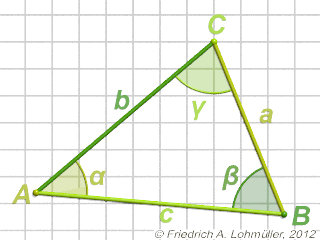
The Law of Cosines
Some useful geometrical facts on the sides and angles of triangles. |
Note: The trigonometric functions sin(X), cos(X) and tan(X) in POV-Ray
need their arguments X in radians !!! The symbole π = pi in POV-Ray.
According to this the reverse fuctions asin(x), acos(x) and atan(x) are giving the angles in radians.
|
For every tiangle ABC we have:
c2 = a2 + b2 - 2*a*b*cos( γ ) (1)
b2 = a2 + c2 - 2*a*c*cos( β ) (2)
a2 = b2 + c2 - 2*b*c*cos( α ) (3)
For γ = 90° = pi/2 (right-angled triangle)
we have cos(γ) = 0 and for this by (1):
c2 = a2 + b2 (Pythagorean Theorem).
-----------------------------------------------------
For the angles of a triangle ABC
we get the following formulas:
γ = acos ( ( a2 + b2 - c2 )/(2*a*b) ) (4)
β = acos ( ( a2 + c2 - b2 )/ (2*a*c) ) (5)
α = acos ( ( b2 + c2 - a2 )/ (2*b*c) ) (6)
|
|
A triangle ABC in 2D.
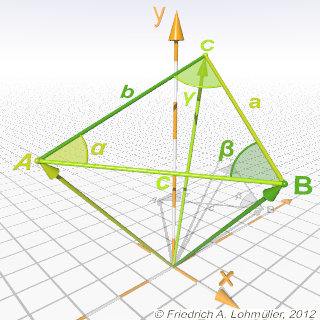
A triangle ABC in 3D.
|
|