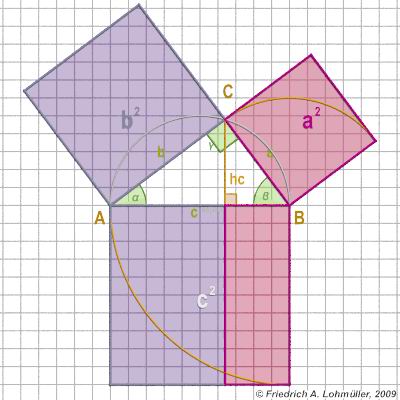
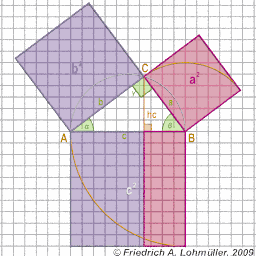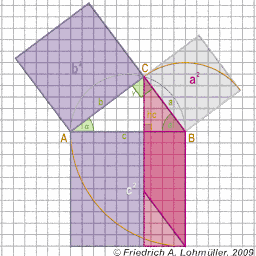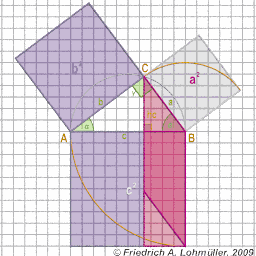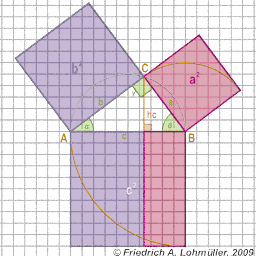
In a right-angled triangle with the hypotenuse c,
and the catheti a and b,
the Pythagorean theoreme says:
a2 + b2 = c2
[In any right triangle, the area of the square whose side is the hypotenuse
(the side opposite the right angle) is equal to the sum of the areas of
the squares whose sides are the two legs (the two sides that meet at a right angle).]
|
Calculations of the sides:
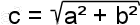
c = sqrt( a*a + b*b ) ; or
c = sqrt( pow( a , 2) + pow( b , 2 ) ) .
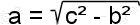
a = sqrt( c*c - b*b ) ;
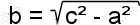
b = sqrt( c*c - a*a ) ;
|
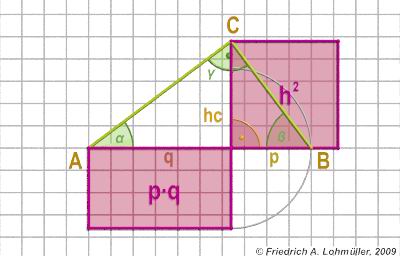
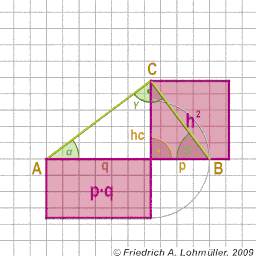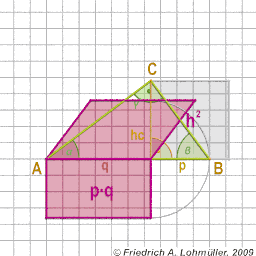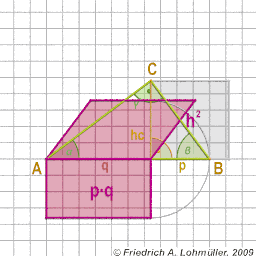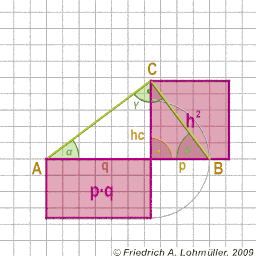
The catheti a and b of right-angled triangle:
a2 = p*c or
b2 = q*c
|
The height hc of right-angled triangle:
h2 = p * q
|
|
The Theorem of Pythagoras at a right-angled triangle
h2 = p * q
|