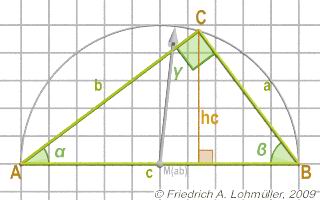
Dimensions and Names
The longest side is the side opposite to the right angle γ at Point C
is called hypotenuse c,
the other two sides are called legs or catheti (singular: cathetus) a and b.
The angle α is at A and ϐ is the angle at B. |
α + ϐ = 90 degrees.
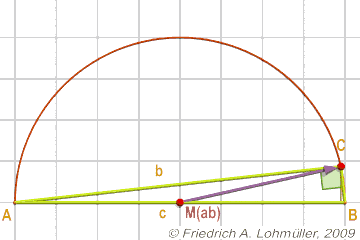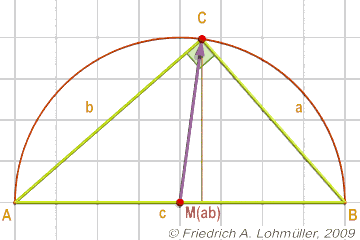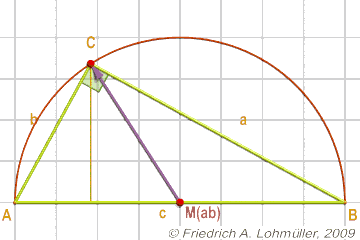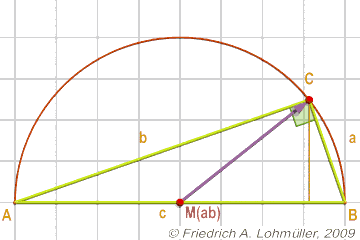
The radius of the circumcircle:
R = 1/2 * c = 1/2* d(A,B);
The median theorem:
A rule for all right triangles:
If MAB is the midpoint of the hypotenuse c, then CMAB = ½ c.
One can also say that point C is located on the circle with diameter [AB].
Conversely, if C is any point of the circle with diameter [AB],
then angle at C in the triangle ABC is a right angle.
|
|
A right-angled triangle
A right-angled triangle, the median theorem
Thales' theorem:
If AB is a diameter, then the angle at C is a right angle.
|