Descriptions et exemples pour le POV-Ray raytracer
par Friedrich A. Lohmueller
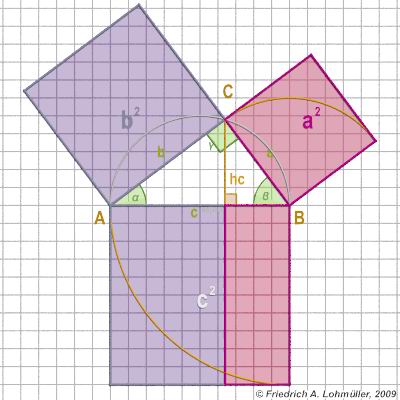
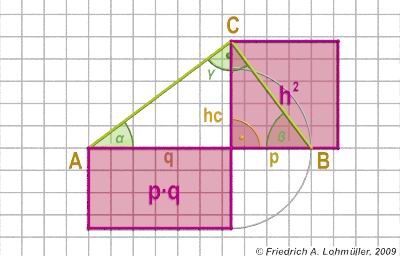
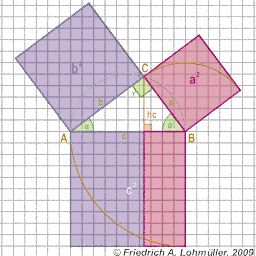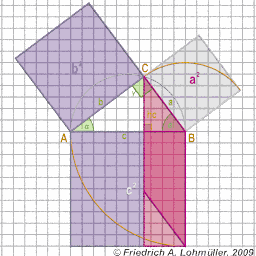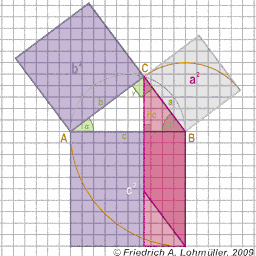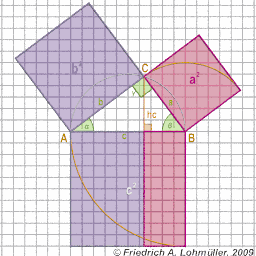
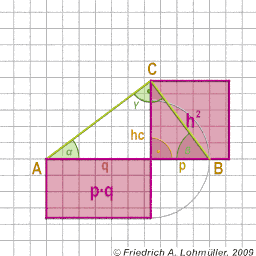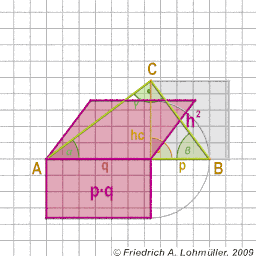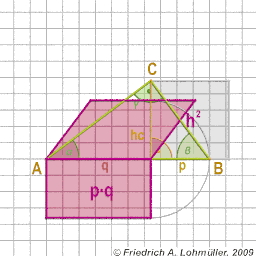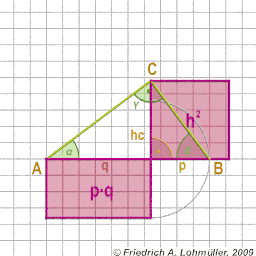
Géométrie de Base -
pour Raytracing
Italiano
Deutsch