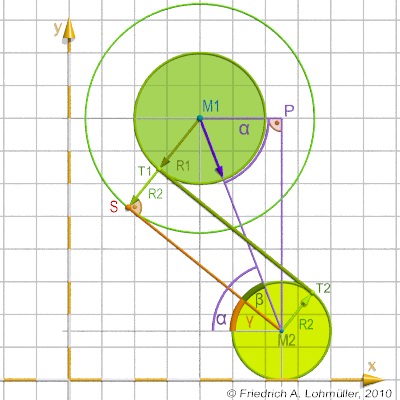
Wir suchen eine interne Tangente an zwei Kreise
von T1 zu T2, wie in nebenstehender Abbildung.
Kreis 1: M1 = <x1,y1,0>, r1.
Kreis 2: M2 = <x2,y2,0>, r2. |
Eine interne Tangente ist parallel zu einer Tangente vom Mittelpunkt des kleineren Kreises (hier: M2)
zum einem Kreis um den Mittelpunkt des größeren Kreises (M1) aber mit dem Radius von r1+r2.
--------------------
Zur Berechnung des Punktes S müssen wir zunächst die Seiten des Dreiecks(M2,M1,S) berechnen.
d(M1,S) = r1+r2 .
Laut des Satz des Pythagoras können wir wie folgt rechnen:
d(M1,M2) = sqrt((x2-x1)2+(y2-y2)2) .
Daher ist die dritte Seite (wieder mit dem Satz des Pythagoras):
d(M2,S) = sqrt( d(M1,S)2+d(M1,M1)2)
Der Winkel zwischen der Richtung von (M1,M2) und der x-Richtung kann man mittels
trigonometrischer Funktionen berechnen.
Wenn x1 < x2 gilt
α = abs(degrees( atan ((y2-y1)/(x2-x1))),
sonst gilt:
α = 180° - abs(degrees( atan ((y2-y1)/(x2-x1))).
Dann berechnen wir β und γ wie folgt:
β = abs( degrees( asin( d(M1, S ) / d(M1,M2) ) )) .
γ = α - β .
Die Position von T1:
xT1 = x1 - r1·cos( Angle(M1S) ).
yT1 = y1 - r1· sin( Angle(M1S) ).
Die Position von T2:
xT2 = x2 + r1·cos( Angle(M1S) ).
yT2 = y2 + r1· sin( Angle(M1S) ).
|
|
Interne Tangenten zweier Kreise gerendert mit POV-Ray
Anmerkung: Um eine Kollision mit fest vordefinierten Bezeichnern und in POV-Ray
reservierten Wörter zu vermeiden,
wird dringend empfohlen als Bezeichner für
Variable und Objekte, welche vom Benutzer definiert werden,
nur Wörter zu verwenden, die mit einem Großbuchstaben beginnen.
D.h. man verwende "R1" anstatt "r1"
und man verwende "Y2" anstelle von "yM2".
#local X1= 0.40; #local Y1= 0.80; #local R1= 0.20;
#local X2= 0.64; #local Y2= 0.15; #local R2= 0.15;
#local M1 = <X1,Y1,0>; #local M2 = <X2,Y2,0>
//------------------------------------------------
#local M_Dist = sqrt(pow(X2-X1,2)+pow(Y2-Y1,2));
#if ( X1 < X2) #local Alpha =
abs( degrees( atan((Y2-Y1)/(X2-X1))));
#else #local Alpha =
180-abs(degrees(atan((Y2-Y1)/(X2-X1))));
#end
#local Beta = abs(degrees(asin((R1+R2)/M_Dist)));
#local Gamma = Alpha - Beta;
#local T1 = M1-<(R1)*cos( radians(Gamma)),
(R1)*sin( radians(Gamma)),0>;
#local T2 = M2+<(R2)*cos( radians(Gamma)),
(R2)*sin( radians(Gamma)),0>; |
Die Berechnung der Tangente von T1 zu T2 in POV-Ray
|