matrix < , , >
Matrices and Affine Mapping
The "matrix"-keyword can be used to define explicit
the transformation matrix for objecte or textures.
The syntax of this keyword:
matrix <m00, m01, m02,
m10, m11, m12,
m20, m21, m22,
m30, m31, m32> |
where the numbers mij
may be all kind of float expressions
They form the elements of the first 3 columns of a 4x4-martrix, with the 4th column
is defined fixed by <0,0,0,1>.
A point P1(x1/y1/z1)
will be mapped to an other point P2(x2/y2/z2)
, by following definition:
x2
= m00*x1
+ m10*y1
+ m20*z1
+ m30
y2 = m01*x1
+ m11*y1
+ m21*z1
+ m31
z2 = m02*x1
+ m12*y1
+ m22*z1
+ m32
|
Somewhat abstract - isn't it?
Here some samples to clear this up:
1) The matrix of the identical mapping:
matrix < 1, 0, 0,
0, 1, 0,
0, 0, 1,
0, 0, 0 > |
|
2) This mtrix causes a parallel translation by the vector <2,3,4>:
matrix < 1, 0, 0,
0, 1, 0,
0, 0, 1,
2, 3, 4 > |
The same, only much more effective and better to understand, is descriped by the statement:
translate< 2, 3, 4>. |
3) Rotation around the y axis with an angle of Alpha (messured in degrees) will be caused by the following matrix:
(Speciality: sin and cos in POVRAY need their arguments for the angle in radians!)
#declare A = radians(Alpha);
matrix<cos(A), 0, sin(A),
0 , 1, 0 ,
-sin(A), 0, cos(A),
0 , 0, 0 > |
Rotation around the y axis by 30°
(sin30° = 0.5; cos30° = 0.886):
matrix <0.886, 0, 0.5,
0 , 1, 0,
-0.5 , 0, 0.886,
0 , 0, 0 > |
The same, only much more effective and better to understand, is descriped by the statement:
rotate< 0, Alpha, 0> .
|
4) The following matrix causes an additional streching by an streching factor of k = 3
with the center in O(0/0/0):
matrix < 3, 0, 0,
0, 3, 0,
0, 0, 3,
0, 0, 0 > |
Also this mapping can be descriped by "scale<3,3,3>"
or more simpler by "scale 3" more easily and easier to understand.
|
These samples have demonstrated that all simple transformations can be descriped by
"matrix".
Normally we don't use transformation matrices for all the simple transformations
(translation, scaling = centric streching, rotation), because it's hard to understand.
But there is an interesting aspect of the matrix statement:
It allows also affine mapping of a more general kind which is not to get in another way,
e.g. the shearing.
The following matrix causes a shearing of an object or a texture along the y axis:
matrix < 1, 1, 0,
0, 1, 0,
0, 0, 1,
0, 0, 0 > |
A shearing along the x direction by factor 0.5 (30°) is caused by: |
matrix< 1 , 0, 0,
0.5, 1, 0,
0 , 0, 1,
0 , 0, 0 > |
|
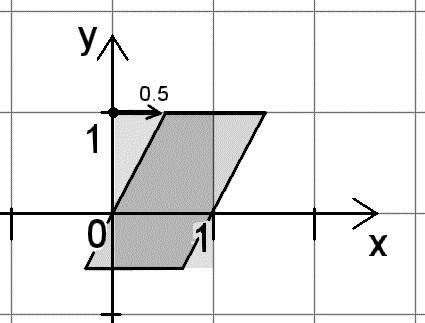
|
The combination of different mappings by matrices are rarely easy to
understand. The following matrix may demonstrate it. This matrix rotates an object around the y axis
by 30 degrees and then it is shearing along the y axis and translates parallel in y direction:
matrix< 0.886, 0.5, 0.5 ,
0 , 1 , 0 ,
0 , 0 , 0.886,
0 , 1.5, 0 > |
This demonstrates why it is recommanded - if you have no intensiv experience with this -
to divide such obscure kind of mappings and to do it step by step:
rotate<0,30,0>
//Shearing in y direction:
matrix<1, 0.5, 0,
0, 1 , 0,
0, 0 , 1,
0, 0 , 0 >
translate<0,1.5,0> |
This statements will do the same!
|


