Home
- POV-Ray Tutorial
Geometric
Transformations
- Index
Elementary
Transformations
- "translate< ... >"
- "rotate< ... >"
- "scale< ... >"
- "scale<-1,1,1>"
Other
Transformations
- "matrix< ... >"
- Shearing
- transforms.inc
- "transform{ ...}"
and "inverse"
Vectors and
Transformations
Insert Menu Add-on
& Download
|
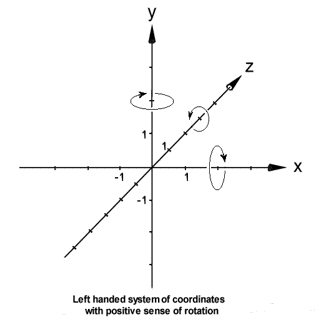
"rotate"
arround one or more axes of the coordinate system
|
|
|
rotate
general syntax:
rotate <wx,wx,wz>
this causes a rotation of an object arround the appropriated coordinate axis of the three basic directions
by an angle of wx degrees arround the x axis
by an angle of wy degrees arround the y axis and
by an angle of wz degrees arround the z axis.
Attention: The rotations are not applied relative of any local axes of symetriy through the center of an object and
the rotations will be applied in the writen order!
|
"rotate< 0,90, 0>" causes a rotation arround the y axis by 90 degrees (lefthanded positive).
"rotate< 0,90,45>" first causes a rotation arround the y axis by 90 degrees and then
a rotation arround the z axis by 45 degrees.
"rotate< 0, 0,45> rotate< 0,90, 0>" first causes a rotation of 45 degrees arround the z axis
followed by a rotation of 90 degrees arround the y axis.
 Attention:
Attention:
Sequential rotations arround different axes
are not interchangeable!
This means the result depends on the order in which we apply these rotations!
High potential of frustration if we are not carefully enough!!!.
 Attention:
Attention:
A rotation by
"rotate < , , >" will be executed always around
the according axes of the system of coordinates!
If we want to turn an object with its center at
<x1,y1,z1> around the direction of
x, y and/or z with rotate<xrot,yrot,zrot>
relative to its center we have to do it in this way:
translate -<x1,y1,z1> // First push it to <0,0,0>! Attention: minus!
rotate<xrot,yrot,zrot> // Then rotate the object and
translate <x1,y1,z1> // then push it back to its position!
|
Sample 1:
|
#declare YellowSmarty =
sphere{<0,0,0>,1
scale <1,0.5,1>
translate<4,0,0>
texture{
pigment{ color rgb<1,0.65,0>}
finish { diffuse 0.9
phong 1}}} //--
object{YellowSmarty rotate<0,0, 90>}
object{YellowSmarty rotate<0,0,105>}
object{YellowSmarty rotate<0,0,120>}
object{YellowSmarty rotate<0,0,135>}
object{YellowSmarty rotate<0,0,150>}
object{YellowSmarty rotate<0,0,165>}
object{YellowSmarty rotate<0,0,180>}
//---------------------------------
#declare Zylinder_1 =
cylinder{<0,0,0>,<0,3,0>,0.2
translate<0,0,5>
texture{
pigment{ color NeonPink}
finish { diffuse 0.9
phong 1}}} //--
object{Zylinder_1 rotate<0, 0,0>}
object{Zylinder_1 rotate<0, 15,0>}
object{Zylinder_1 rotate<0, 30,0>}
object{Zylinder_1 rotate<0, 45,0>}
object{Zylinder_1 rotate<0, 60,0>}
object{Zylinder_1 rotate<0, 75,0>}
object{Zylinder_1 rotate<0, 90,0>}
object{Zylinder_1 rotate<0,105,0>}
object{Zylinder_1 rotate<0,120,0>}
object{Zylinder_1 rotate<0,135,0>}
object{Zylinder_1 rotate<0,150,0>}
object{Zylinder_1 rotate<0,165,0>}
object{Zylinder_1 rotate<0,180,0>}
//---------------------------------- |
|
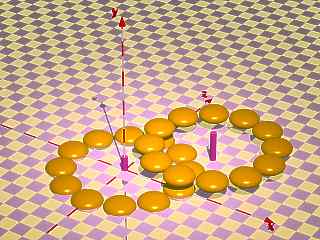
Sample 2:
|
#declare Ring=
union{
object{YellowSmarty rotate<0, 0,0>}
object{YellowSmarty rotate<0, 30,0>}
object{YellowSmarty rotate<0, 60,0>}
object{YellowSmarty rotate<0, 90,0>}
object{YellowSmarty rotate<0,120,0>}
object{YellowSmarty rotate<0,150,0>}
object{YellowSmarty rotate<0,180,0>}
object{YellowSmarty rotate<0,210,0>}
object{YellowSmarty rotate<0,240,0>}
object{YellowSmarty rotate<0,270,0>}
object{YellowSmarty rotate<0,300,0>}
object{YellowSmarty rotate<0,330,0>}
cylinder{<0,-1,0>,<0,1,0>,0.2
texture{
pigment{ color NeonPink}
finish { diffuse 0.9
phong 1} } }
}// end of union //---------------
object{Ring}
object{Ring translate<4,1,4> }
//-------------------------------- |
|
Hint:
"rotate" can also be used with geometric shapes as well as with other objects like light sources, textures("texture"),
color patterns ("pigment") and simulated surface deformations ("normal").
|
|