Home
- POV-Ray Tutorial
Schleifen,
Sinus, Kosinus
und POV-Ray
>1. Lineare Wellen
2. Jetzt geht's rund!
3. Fliegende
Teppiche
- Download
|
Sinus und Kosinus linear
|
Diese Beschreibung möchte einige Spielereien mit der
Sinus- bzw. Kosinus-Funktion demonstrieren. Das hierbei wichtigste über
Schleifen soll das folgende Beispiel kurz an einer doppelt ineinander
geschachtelten Schleife demonstrieren.
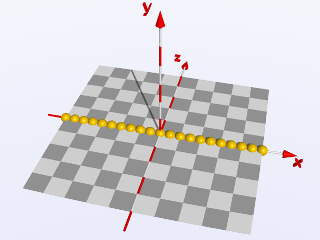
Betrachten wir hier erst einmal eine einfache Schleife, welche
kleine Kugeln längs der x-Achse von x = 5 bis x = +5 plaziert:
|
#declare Ball =
sphere{<0,0,0>,0.25
texture{
pigment{color rgb<1,0.8,0>}
finish {diffuse 0.9 phong 1}
}// end of texture
}// end of sphere
#declare X = -5; // Start-Wert X
#declare EndX = 5; // End-Wert X
#declare Step = 0.5;//Schrittweite
// Schleifen-Anfang :
#while ( X < EndX + Step)
object{ Ball translate <X,0,0> }
#declare X = X+Step; // next X-Wert
#end // ------------ Schleifen-Ende |
|
|
|
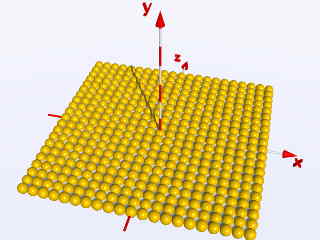
Packt man die vorhandene Schleife, in ein eine weitere Schleife,
welche die z-Wert von z = -5 bis z = +5 durchläuft, so erhält
man eine von Kugeln bedeckte quadratische Fläche:
|
#declare Z = -5; // Start-Wert Z
#declare EndZ = 5; // End-Wert Z
#declare Step = 0.5;//Schrittweite
//---- Schleifen-Anfang Z :
#while ( Z < EndZ + Step)
#declare X = -5; // Start-Wert X
#declare EndX = 5; // End-Wert X
//------ Schleifen-Anfang X :
#while ( X < EndX + Step)
object{ Ball translate <X,0,Z>}
#declare X = X+Step;//next X-Wert
#end // -------- Schleifen-Ende X
#declare Z = Z+Step; //next Z-Wert
#end // ---------- Schleifen-Ende Z |
|
|
|
Soweit die zum folgenden notwendige Schnellwäsche in Sachen
Schleifen!
Jetzt wollen wir mal etwas Bewegung in die Fläche bringen. Dazu
benötigen wir die Sinus- bzw. Kosinus Funktion, welche in POV-Ray
mit sin(A) bzw. cos(A)
bezeichnet wird und als Argument A den Winkelwert in Radiant
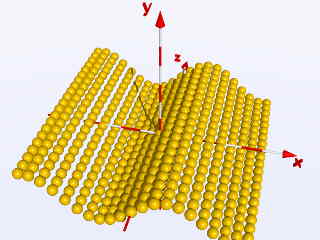
benötigt. Wandelt man obige Doppelschleife wie folgt ab:
object{ Ball translate < X,
sin(X), Z> }
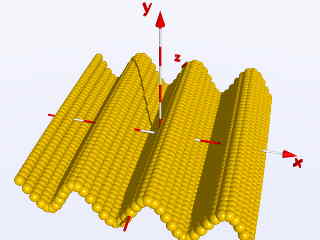
bzw. mit halber Schrittweite Step = 0.25
object{ Ball translate < X,
sin(2*X), Z> }
ergeben sich folgende Bilder:
|
|